Writing a calculator is a simple task - just add nine buttons labeled 1-9 and add a plus and minus button and we’re almost good to go. In this entry I’m going to write a calculator called SimpleCalc that does not have a GUI, instead it’ll take in an arbitrary expression and calculate the results of it. The input I’ll use as my immediate goal is the following:
25-37+2*(1.22+cos(5))*sin(5)*2+5%2*3*sqrt(5+2)
According to Google the result is -9.83033875. Some of the tricky subjects we’ll have to handle is operator precedence (multiplication before addition etc), nested expressions (2*1.22+cos(5) != 2*(1.22+cos(5))) and associativity (5+7 == 7+5 & 7-5 != 5-7 etc).
Parsing the input using SableCC
Before doing any calculations, we need to parse the input expression so we have an in-memory representation of the input. We need to have the input represented in the form of an abstract syntax tree that defines the order of operations and allows us to traverse the different parts of the expression individually. To perform this task, we’ll be using SableCC.
SableCC is a parser generator which generates fully featured object-oriented frameworks for building compilers, interpreters and other text parsers. In particular, generated frameworks include intuitive strictly-typed abstract syntax trees and tree walkers. SableCC also keeps a clean separation between machine-generated code and user-written code which leads to a shorter development cycle.
In short, SableCC can be used to automatically generate the parser code that’s used in any compiler, as well as in a lot of other cases where input needs to be parsed - like in this case. SableCC itself is written in Java by Etienne M. Gagnon and the source code is freely available.
The standard output from SableCC is Java code. Thus, the parser we’re about to generate will be made into a number of Java files that we can incorporate into our own source code and extend. As I’ll be writing the calculator in C#, I’d much prefer to work with C# source files directly, rather than having to port the Java output or call it by other means. Luckily Indrek Mandre has made a SableCC variant that’ll generate the parser in either Java, C#, C++, O’Caml, Python, C, Graphviz Dot or XML. All we need to do is to download the sablecc-3-beta.3.altgen.20041114 zip file from the frontpage of Indrek’s SableCC page. Once it’s downloaded and unpacked we’re able to run it, as long as Java is installed. First create a bat file with the following contents:
java -jar "C:Program FilesSableCCsablecc-3-beta.3.altgen.20041114libsablecc.jar" %1 %2 %3 %4 %5 %6 %7 %8 %9
Make sure to replace my path with whatever path you’ve extracted the SableCC altgen package into. When we invoke SableCC from now on, we’ll do it through this bat file that I’ve chosen to call sablecc_altgen.bat, just to make the syntax simpler.
Defining the grammar
For SableCC to be able to generate our parser, we first need to define the language it should support. The way we do this is to define the language in the (E)BNFformat. I won’t be writing a generic tutorial on how to write grammers in SableCC as there’s already a number of good ones on the SableCC Documentation page, as well as one by Nat Pryce that’s not on the documentation page. Finally there’s also a mailing list, though the activity is limited.
We’ll start out by creating a new text file called simplecalc.sablecc, this is where we’ll be defining our SimpleCalc grammar. Furthermore I’ve created a new bat file called simplecalc_sable.bat with the following contents:
cls
sablecc_altgen -d generated -t csharp simplecalc.sablecc
The above bat file will call the one we previously made. -d generated specifies the output directory name. -t csharp specifies the output source code type, C# in this case. The last argument is the name of the input sablecc file. From now on we can simply run simplecalc_sable to start the SableCC compilation process.
I’ll post the full simplecalc.sablecc file contents first, and then go through the specific sections one by one afterwards.
Package SimpleCalc;
Helpers
digit = ['0' .. '9'];
Tokens
number = (digit+ | digit+ '.' digit+);
add = '+';
sub = '-';
mul = '*';
div = '/';
mod = '%';
sqrt = 'sqrt';
cos = 'cos';
sin = 'sin';
lparen = '(';
rparen = ')';
Productions
exp {-> exp}
= {add} [left]:exp add [right]:factor {-> New exp.add(left, right.exp)}
| {sub} [left]:exp sub [right]:factor {-> New exp.sub(left, right.exp)}
| {factor} factor {-> factor.exp}
;
factor {-> exp}
= {mul} [left]:factor mul [right]:unary {-> New exp.mul(left.exp, right.exp)}
| {div} [left]:factor div [right]:unary {-> New exp.div(left.exp, right.exp)}
| {mod} [left]:factor mod [right]:unary {-> New exp.mod(left.exp, right.exp)}
| {unary} unary {-> unary.exp}
;
unary {-> exp}
= {number} number {-> New exp.number(number)}
| {sqrt} sqrt lparen exp rparen {-> New exp.sqrt(exp)}
| {cos} cos lparen exp rparen {-> New exp.cos(exp)}
| {sin} sin lparen exp rparen {-> New exp.sin(exp)}
| {paren} lparen exp rparen {-> New exp.paren(exp)}
;
exp_list {-> exp*}
= {single} exp {-> [exp.exp]}
| {multi} exp [tail]:exp_list {-> [exp.exp, tail.exp]}
;
Abstract Syntax Tree
exp
= {add} [left]:exp [right]:exp
| {sub} [left]:exp [right]:exp
| {mul} [left]:exp [right]:exp
| {div} [left]:exp [right]:exp
| {mod} [left]:exp [right]:exp
| {paren} exp
| {sqrt} exp
| {cos} exp
| {sin} exp
| {number} number
;
In the grammar we’re using 5 different sections, Package, Helpers, Tokens, Productions and Abstract Syntax Tree.
Package SimpleCalc;
The Package declaration simply defines the name of the overall package. If this is excluded (which is valid according to SableCC) our namesapces int he generated C# code will be blank and thus invalid.
Helpers
digit = ['0' .. '9'];
Helpers are basically placeholders you can setup and use throughout the SableCC file. They have no deeper meaning or functionality, it’s just a way to easily be able to express common code by its name. As we’ll be referring to digits multiple times it helps to define it as a helper instead of replicating [‘0’ .. ‘9’] multiple times in the code. [‘0’ .. ‘9’] means all digits between 0 and 9.
Tokens
number = (digit+ | digit+ '.' digit+);
add = '+';
sub = '-';
mul = '*';
div = '/';
mod = '%';
sqrt = 'sqrt';
cos = 'cos';
sin = 'sin';
lparen = '(';
rparen = ')';
Note that I’m jumping ahead and ignoring Productions section for now, I’ll come to that in just a bit. The Abstract Syntax Tree defines the nodes that will be present in our parsed AST. Each type of operation and function has a corresponding node in the AST. Thus, and add operation will consist of an Add node with two children - a left and a right expression. Those expressions may themselves be constant numbers or nested expressions - since they’re defined as exp which is a recursive reference to the actual AST exp type.
Add, sub, mul, div and mod are binary operators and thus have two child expressions. Paren, sqrt, cos and sin (and in some ways, number) are unary operators in that they only have a single child/parameter - an expression. Number is a leaf node that expresses an actual number constant.
The Productions section defines our mapping from the actual input to the AST that we’ve just defined.
Productions
exp {-> exp}
= {add} [left]:exp add [right]:factor {-> New exp.add(left, right.exp)}
| {sub} [left]:exp sub [right]:factor {-> New exp.sub(left, right.exp)}
| {factor} factor {-> factor.exp}
;
The first production we define is a generic one for expressing expressions. Note that the way we define operator precedence is by first expressing the least prioritized operator (add & sub) and then referencing the factor operations (mul, div, mod & unary) and thus forth. exp {-> exp} signifies that the concrete syntax of an expression is mapped into the abstract syntax tree node called “exp” as well. Productions and Abstract Syntax Tree are two different namespaces and they may thus share the same names.
= {add} [left]:exp add [right]:factor {-> New exp.add(left, right.exp)}
The add operation is defined by a left expression followed by the add token (defined as ‘+’ previously) and then a factor expression on the right, hence defining the precedence relation between the add operation and factor operations. Finally we define that the add operation maps into a new instance of the exp AST node, having the left and right expressions as parameters (children in the AST). The sub operation is almost identical to the add operator.
| {factor} factor {-> factor.exp}
Any factor expressions are simply mapped onto the factor production defined later on.
factor {-> exp}
= {mul} [left]:factor mul [right]:unary {-> New exp.mul(left.exp, right.exp)}
| {div} [left]:factor div [right]:unary {-> New exp.div(left.exp, right.exp)}
| {mod} [left]:factor mod [right]:unary {-> New exp.mod(left.exp, right.exp)}
| {unary} unary {-> unary.exp}
;
The mul, div and mod expressions are basically identical to the add and sub expressions, except defining unary as the next production in the operator precedence chain.
unary {-> exp}
= {number} number {-> New exp.number(number)}
| {sqrt} sqrt lparen exp rparen {-> New exp.sqrt(exp)}
| {cos} cos lparen exp rparen {-> New exp.cos(exp)}
| {sin} sin lparen exp rparen {-> New exp.sin(exp)}
| {paren} lparen exp rparen {-> New exp.paren(exp)}
;
The simplest of all expressions is the unary number expression that defines a numeric constant. The number expression is mapped into a new AST node of the type exp.number, having the actual number as a parameter. The sqrt, cos and sin functions all define the input as the function name and the parameter expression enclosed in parentheses. Finally we define the {paren} unary function which is an arbitrary expression enclosed in parentheses. This gets mapped into the exp.paren AST type, taking the arbitrary expression as a parameter. The {paren} function allows us to differentiate between expressions like “5*2-7” and “5*(2-7)”.
exp_list {-> exp*}
= {single} exp {-> [exp.exp]}
| {multi} exp [tail]:exp_list {-> [exp.exp, tail.exp]}
;
The final production is what allows us to chain expressions. Without the exp_list production only single operations would be allowed (5+2, 3*7 etc), not chains of expressions (5+2+3, 5*2+3 etc). exp_list {-> exp*} defines that the exp_list production maps into a list of exp’s in the AST.
Anyone having done functional programming will recognize the tail recursion going on here. If there’s only a single expression, we map it into a list of expressions containing just that one expression. If there’s a single expression and a list of expressions following it (which may be one or more expressions), we map it into a list of expressions containing the first expression as well as the rest of the expressions represented by the tail parameter.
Generating the parser
Once we’ve defined the grammar, we’re ready to run the simplecalc_sable bat file, hopefully resulting in the following output:
D:\Webmentor Projekter\Eclipse Projects\SableCC\>simplecalc_sable -d generated -t c
sharp simplecalc.sablecc
D:\Webmentor Projekter\Eclipse Projects\SableCC\>java -jar "C:Program FilesSabl
eCCsablecc-3-beta.3.altgen.20041114libsablecc.jar" -d generated -t csharp sim
plecalc.sablecc
SableCC version 3-beta.3.altgen.20040327
Copyright (C) 1997-2003 Etienne M. Gagnon <etienne.gagnon@uqam.ca> and
others. All rights reserved.
This software comes with ABSOLUTELY NO WARRANTY. This is free software,
and you are welcome to redistribute it under certain conditions.
Type 'sablecc -license' to view
the complete copyright notice and license.
-- Generating parser for simplecalc.sablecc in D:Webmentor ProjekterEclipse P
rojectsSableCCgenerated
Verifying identifiers.
Verifying ast identifiers.
Adding empty productions and empty alternative transformation if necessary.
Adding productions and alternative transformation if necessary.
computing alternative symbol table identifiers.
Verifying production transform identifiers.
Verifying ast alternatives transform identifiers.
Generating token classes.
Generating production classes.
Generating alternative classes.
Generating analysis classes.
Generating utility classes.
Generating the lexer.
State: INITIAL
- Constructing NFA.
..............................
- Constructing DFA.
...................................................
....................
- resolving ACCEPT states.
Generating the parser.
..............................
..............................
..............................
..
..............................
Now if we look in the generated directory, there should be six files: analysis.cs, lexer.cs, nodes.cs, parser.cs, prods.cs and tokens.cs. The files should contain classes in the SimpleCalc namespace.
Printing the abstract syntax tree
To help ourselves, the first task we’ll do is to simply print out the AST so we can verify what gets parsed is correct. Create a solution called SimpleCalc and either copy the genrated files or create a solution link to the folder. Add a new file called AstPrinter.cs and paste the following contents:
using System;
using SimpleCalc.analysis;
using SimpleCalc.node;
namespace SimpleCalc
{
class AstPrinter : DepthFirstAdapter
{
int indent;
private void printIndent()
{
Console.Write("".PadLeft(indent, 't'));
}
private void printNode(Node node)
{
printIndent();
Console.ForegroundColor = ConsoleColor.White;
Console.Write(node.GetType().ToString().Replace("SimpleCalc.node.", ""));
if (node is ANumberExp)
{
Console.ForegroundColor = ConsoleColor.DarkGray;
Console.WriteLine(" " + node.ToString());
}
else
Console.WriteLine();
}
public override void DefaultIn(Node node)
{
printNode(node);
indent++;
}
public override void DefaultOut(Node node)
{
indent--;
}
}
}
The DepthFirstAdapter is a class auto generated by SableCC. It allows us to easily traverse the generated AST depth first, while giving us various hook points along the way. Each node in the tree has an In and Out method that we can override. In is called before the children are traversed while Out is called after the children have been traversed. Note that we may change the tree during the traversal - though we’re not going to do so.
In the AstPrinter class I’ve overriden the DefaultIn and DefaultOut methods that gets called for each node unless we’ve overriden their specific default methods. In the In method we increase the indent, and likewise we decrease it in the Out method. Furthermore, in the In method we also print the actual node contents to the console. If it’s a ANumberExp node (the name of the node corresponding to the number type in the AST) then we print the actual number, otherwise we just print the name of the node itself.
In the main program file, paste the following:
using System;
using System.IO;
using SimpleCalc.lexer;
using SimpleCalc.node;
using SimpleCalc.parser;
namespace SimpleCalc
{
class Program
{
private static void Main(string[] args)
{
if (args.Length != 1)
exit("Usage: Simplecalc.exe filename");
using (StreamReader sr = new StreamReader(File.Open(args[0], FileMode.Open)))
{
// Read source
Lexer lexer = new Lexer(sr);
// Parse source
Parser parser = new Parser(lexer);
Start ast = null;
try
{
ast = parser.Parse();
}
catch (Exception ex)
{
exit(ex.ToString());
}
// Print tree
AstPrinter printer = new AstPrinter();
ast.Apply(printer);
}
exit("Done");
}
private static void exit(string msg)
{
if (msg != null)
Console.WriteLine(msg);
else
Console.WriteLine();
Console.WriteLine("Press any key to exit...");
Console.Read();
Environment.Exit(0);
}
}
}
I’ve made it so the program takes in a single argument, a filename where our calculation expression is written. By taking a file as a parameter, it’s easier for me to change the expression directly in Visual Studio without having to setup launch parameters. The only launch parameter that needs to be set is the file argument.
The program tries to open the file and then instantiates the SableCC auto generated lexer and parser.
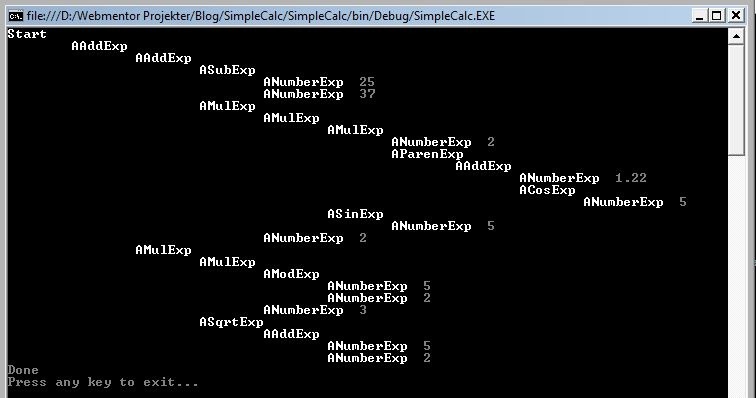
Now let’s make a new file called test.ss and paste the following expression into it: 25-37+2*(1.22+cos(5))*sin(5)*2+5%2*3*sqrt(5+2). If you run the application at this point, you should see an output like the following:
By comparing the printed AST with the input expression, we’ll see that they match both in contents and in regards to operator precedence. Now all that’s left is to perform the actual calculation of the expression.
Calculating the expression based on the abstract syntax tree
Add a new file called AstCalculator.cs and paste the following contents:
using System;
using System.Collections.Generic;
using System.Globalization;
using SimpleCalc.analysis;
using SimpleCalc.node;
namespace SimpleCalc
{
class AstCalculator : DepthFirstAdapter
{
private double? result;
private Stack<double> stack = new Stack<double>();
public double CalculatedResult
{
get
{
if (result == null)
throw new InvalidOperationException("Must apply AstCalculator to the AST first.");
return result.Value;
}
}
public override void OutStart(Start node)
{
if (stack.Count != 1)
throw new Exception("Stack should contain only one element at end.");
result = stack.Pop();
}
// Associative operators
public override void OutAMulExp(AMulExp node)
{
stack.Push(stack.Pop() * stack.Pop());
}
public override void OutAAddExp(AAddExp node)
{
stack.Push(stack.Pop() + stack.Pop());
}
// Non associative operators
public override void OutASubExp(ASubExp node)
{
double numB = stack.Pop();
stack.Push(stack.Pop() - numB);
}
public override void OutAModExp(AModExp node)
{
double numB = stack.Pop();
stack.Push(stack.Pop() % numB);
}
public override void OutADivExp(ADivExp node)
{
double numB = stack.Pop();
stack.Push(stack.Pop() / numB);
}
// Unary
public override void OutASqrtExp(ASqrtExp node)
{
stack.Push(Math.Sqrt(stack.Pop()));
}
public override void OutACosExp(ACosExp node)
{
stack.Push(Math.Cos(stack.Pop()));
}
public override void OutASinExp(ASinExp node)
{
stack.Push(Math.Sin(stack.Pop()));
}
public override void InANumberExp(ANumberExp node)
{
stack.Push(Convert.ToDouble(node.GetNumber().Text.Trim(), new CultureInfo("en-us")));
}
}
}
I will not go through all parts of the calculator as many functions are very similar. I’ll outline the important ones below.
private double? result;
private Stack<double> stack = new Stack<double>();
public double CalculatedResult
{
get
{
if (result == null)
throw new InvalidOperationException("Must apply AstCalculator to the AST first.");
return result.Value;
}
}
As all numbers are treated as doubles, the result will be a double as well. The result can be retrieved through the CalculatedResult property, but only once the calculation has been performed - thus we check whether the result is null or not.
While traversing the AST to perform the calculations we maintain state through the use of a generic stack of doubles.
public override void OutStart(Start node)
{
if (stack.Count != 1)
throw new Exception("Stack should contain only one element at end.");
result = stack.Pop();
}
When starting out the stack will be empty. Once we’ve traversed the tree the stack should only contain a single element - the result. To ensure there’s no errors we make sure the stack only contains a single element, after which we return it by popping it from the stack.
public override void InANumberExp(ANumberExp node)
{
stack.Push(Convert.ToDouble(node.GetNumber().Text.Trim(), new CultureInfo("en-us")));
}
Probably the most important unary operator is the constant number. Whenever we’re in a ANumberExp node we read in the number and push it onto the stack.
public override void OutASqrtExp(ASqrtExp node)
{
stack.Push(Math.Sqrt(stack.Pop()));
}
The other unary operators follow the same pattern. We pop the stack and perform a math operation on the popped value, after which we push the result back onto the stack.
public override void OutAMulExp(AMulExp node)
{
stack.Push(stack.Pop() * stack.Pop());
}
The associative operators are simple in that they have no requirements as to which order the input parameters are in. As such, a multiplication simple pops two numbers from the stack and push the multiplied result back onto the stack.
public override void OutASubExp(ASubExp node)
{
double numB = stack.Pop();
stack.Push(stack.Pop() - numB);
}
The non associative opreators need to first pop one number and store it in a temporary variable. The reason we need to do this is that we’re working with a FIFO stack, meaning the second number will not be the topmost on the stack and thus we can’t perform the calculation in a single expression.
Now that we’ve made the AstCalculator class we just need to modify the main method so it runs the calculator.
// Print tree
AstPrinter printer = new AstPrinter();
ast.Apply(printer);
// Calculate expression
AstCalculator calculator = new AstCalculator();
ast.Apply(calculator);
Console.WriteLine("Calculation result: " + calculator.CalculatedResult);
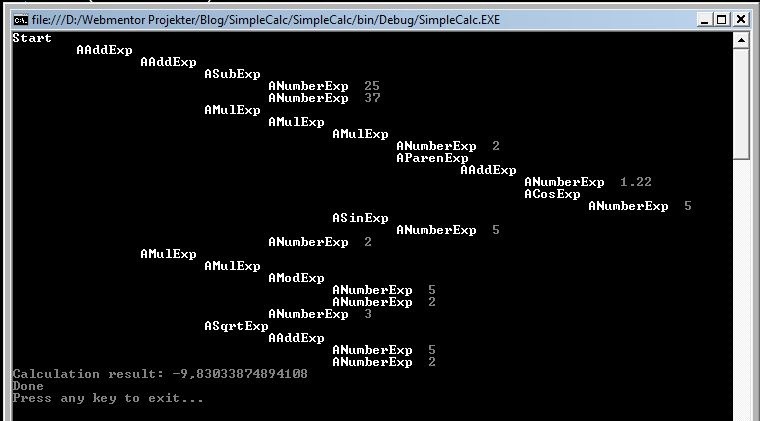
Simply instantiate a new AstCalculator after printing the AST, and then apply it to the AST. If you make the above modification and run the program, you should see an output similar to this:
Lo and behold, the result is identical to the one provided by Google originally!
Wrapping up
I’ve now shown how we can define a language grammar in SableCC and have it auto generate a parser for us. Using the SableCC parser we can read an input string and transform it into an abstract syntax tree. Once we have the abstract syntax tree, we can easily traverse it and modify it.
While SableCC originally was only able to generate Java output, we now have multiple options for the output language. Unfortunately the generated C# classes are not partial - a feature that would’ve been very useful once we start doing more advanced stuff with the AST. It’s rather easy to modify the six source files manually, as well as setting up an automated script to do it for us.
Once we read the input and transformed it into an AST we used stack based approach to traverse it and calculate sub results in a very simple way, emulating how most higher level languages work internally.
I’ll be following up on this post later on by extending the grammar and interpreter functionality.