Implementing a Simple Genetic Algorithm

In this blog post I’ll give a quick introduction to what genetic algorithms are and what they can be used for. We’ll implement a genetic algorithm that attempts to guess an RGB color by evolving upon a random set of initial guesses, until it at some point evolves into the correct RGB value.

What are genetic algorithms?

Contrary to other types of algorithms, genetic algorithms do not have a clear path of improvement for solution candidiates, and it’s not an exhaustive search. A genetic algorithm requires a few base components:

• A representation of a candidate solutions.
• A way of calculating the correctness of a candidate solution, commonly referred to as the fitness function.
• A mutation function that changes a candidate solution slightly, in an attempt to obtain a better candidate.

There are many different ways of implementing genetic algorithms, and there are usually many variables to adjust in a genetic algorithm. How large should the initial population be? How many solutions survives each generation? How do the survivors reproduce? In reproduction, does each survivor give birth to a single child, or multiple? As is noticeable from the terminology, genetic algorithms closely simulate biology.

The building blocks

What we’re trying to accomplish with this demo implementation, is to guess a random RGB value. The RGB values are stored in what is basically a triple class. The only added functionality is an override of the ToString function to make it easier for us to print the solution candidates.

class Rgb
{
	internal int R { get; set; }
	internal int G { get; set; }
	internal int B { get; set; }

	public override string ToString()
	{
		return string.Format("({0}, {1}, {2})", R, G, B);
	}
}

Next up, we have an interface that represents a basic chromosome. In this implementation, a chromosome is basically a candidate solution. The chromosome is also the type that implements the fitness function, to evaluate it’s own correctness. The fitness is returned as an arbitrary double value, the higher the value the better a candidate. The ChromosomeValue property is the actual value being tested - in this case, an instance of Rgb.

interface IChromosome<T>
{
	double Fitness { get; }
	T ChromosomeValue { get; }
}

Template based genetic algorithm

I’ve implemented the genetic algorithm using the template pattern for easy customization and implementation of the algorithm. The algorithm itself is an abstract generic class. This means we have to subtype it before we can use it, a requirement due to the abstract template based implementation.

public abstract class GeneticAlgorithm<T>

There’s a number of properties that are rather self explanatory, given the commenting.

/// <summary>
/// This is the amount of chromosomes that will be in the population at any generation.
/// </summary>
protected int ChromosomePopulationSize;

/// <summary>
/// This is the number of chromosomes that survive each generation, after which they're mutated.
/// </summary>
protected int GenerationSurvivorCount;

/// <summary>
/// This list holdes the chromosomes of the current population.
/// </summary>
protected IList<IChromosome<T>> ChromosomePopulation;

/// <summary>
/// This is the current generation number. Incremented each time a new generation is made.
/// </summary>
public int CurrentGenerationNumber;

/// <summary>
/// This is the current generation population.
/// </summary>
public IEnumerable<IChromosome<T>> CurrentGenerationPopulation
{
	get { return ChromosomePopulation.AsEnumerable(); }
}

The constructor takes in two parameters, the size of the population at any given generation, as well as the number of survivors when an evolution is performed - and a new generation is created, based on the survivors of the old generation.

Lastly, we set the current generation as generation number 1, and then we call createInitialChromosomes to instantiate the initial generation 1 population.

/// <summary>
/// Initializes the genetic algorithm by evolving the initial generation of chromosomes.
/// </summary>
/// <param name="chromosomePopulationSize">The size of any generation.</param>
/// <param name="generationSurvivorCount">The number of chromosomes to survive the evolution of a generation.</param>
public GeneticAlgorithm(int populationSize, int generationSurvivorCount)
{
	if (generationSurvivorCount >= populationSize)
		throw new ArgumentException("The survival count of a generation must be smaller than the population size. Otherwise the population will become stagnant");

	if (generationSurvivorCount < 2)
		throw new ArgumentException("Where would we be today if either Adam or Eve were alone?");

	ChromosomePopulationSize = populationSize;
	GenerationSurvivorCount = generationSurvivorCount;

	// Create initial population and set generation
	CurrentGenerationNumber = 1;
	createInitialChromosomes();
}

The createInitialChromosome initializes the ChromosomePopulation list, and then it’ll continue adding new chromosomes to it until the current population reaches the specified ChromosomePopulationSize. The initial random chromosomes are returned from the CreateInitialRandomChromosome function.

/// <summary>
/// Creates the initial population of random chromosomes.
/// </summary>
private void createInitialChromosomes()
{
	ChromosomePopulation = new List<IChromosome<T>>();

	for (int i = 0; i < ChromosomePopulationSize; i++)
		ChromosomePopulation.Add(CreateInitialRandomChromosome());
}

There are three abstract methods that must be implemented by any subclass, CreateInitialRandomChromosome being one of them. I’ll go over the actual implementations later on.

/// <summary>
/// Creates an arbitrary number of mutated chromosomes, based on the input chromosome.
/// </summary>
protected abstract IEnumerable<IChromosome<T>> Mutate(IChromosome<T> chromosome);

/// <summary>
/// Creates a single random chromosome for the initial chromosome population.
/// </summary>
protected abstract IChromosome<T> CreateInitialRandomChromosome();

/// <summary>
/// Selects the surviving chromosomes of the current generation.
/// </summary>
/// <returns>Returns a list of survivors of the current generation.</returns>
protected abstract IEnumerable<IChromosome<T>> GetGenerationSurvivors();

The last method that’s implemented in the abstract GeneticAlgorithm class is PerformEvolution. PerformEvolution will create a new population for the next generation. First the survivors of the old generation are selected by calling the GetGenerationSurvivors method, which is to be implemented by a subclass. All survivors of the old generation are automatically added to the new generation population.

Then we’ll select a random survivor based on an weighted average of their fitness. The randomly selected survivor will be mutated, and the result of the mutation is added to the new generation population. The Mutate function may return an arbitrary number of results, so technically a single survivor could be the parent of all children in the new generation.

Finally we set the current population and increment the generation number.

/// <summary>
/// Performs an evolution by picking up the generation survivors and mutating them.
/// </summary>
public void PerformEvolution()
{
	IList<IChromosome<T>> newGeneration = new List<IChromosome<T>>();

	// Get the survivors of the last generation
	IEnumerable<IChromosome<T>> survivors = GetGenerationSurvivors();

	// Add the survivors of the previous generation
	foreach (var survivor in survivors)
		newGeneration.Add(survivor);

	// Until the population is full, add a new mutation of any two survivors, selected by weighted random based on their fitness.
	Random rnd = new Random();

	while (newGeneration.Count < ChromosomePopulationSize)
	{
		// Get two random survivors, weighted random sort based on fitness
		var randomSurvivor = survivors
			.OrderBy(c => rnd.NextDouble() * c.Fitness)
			.First();

		foreach (var offspring in Mutate(randomSurvivor))
		{
			if (newGeneration.Count == ChromosomePopulationSize)
				break;

			newGeneration.Add(offspring);
		}
	}

	// Overwrite current population
	ChromosomePopulation = newGeneration;

	// Increment the current generation
	CurrentGenerationNumber++;
}

The rgb guessing implementation

The actual implementation is a class inheriting from GeneticAlgorithm, specifying Rgb as the generic type we’ll be working with.

class RgbGuesser : GeneticAlgorithm<Rgb>

The constructor just calls the base class directly, specifying the population size to be 100, and that there should be 10 survivors of each generation.

public RgbGuesser()
	: base(100, 10)
{ }

The CreateInitialRandomChromosome method just returns a new Rgb instance with random R, G and B vlaues between 1 and 255.

protected override IChromosome<Rgb> CreateInitialRandomChromosome()
{
	return new RgbChromosome(random.Next(1, 256), random.Next(1, 256), random.Next(1, 256));
}

I’ve implemented an optimization that makes sure the most fit candidate chromosome is always included in the survivors of each generation. This’ll make sure we’ll never have a new generation with a worse candidate solution that the last.

After returning the top candidate, we then return the remaining candidates based on a weighted random selection of the remaining population. The reason why we’re not just returning the “top GenerationSurvivorCount” chromosomes is to avoid premature convergence. Premature convergence is basically a fancy way to describe inbreeding. When our gene pool diversity is limited, so is the range of candidates that may come out of it. It’s not a really big issue in the RGB guessing implementation, but premature convergence can be a big issue in other implementations - especially depending on the mutation implementation.

protected override IEnumerable<IChromosome<Rgb>> GetGenerationSurvivors()
{
	// Return the best chromosome
	var topChromosome = this.ChromosomePopulation
		.OrderByDescending(c => c.Fitness)
		.First();

	// Return the remaining chromosomes from the pool
	var survivors = this.ChromosomePopulation
		.Where(c => c != topChromosome)
		.OrderByDescending(c => random.NextDouble() * c.Fitness)
		.Take(this.GenerationSurvivorCount - 1);

	yield return topChromosome;

	foreach (var survivor in survivors)
		yield return survivor;
}

The final method to implement is the Mutate method. This is the one that’s responsible for mutating a survivor into a new candidate solution that’ll hopefully be better than the last. The implementation is really simple. We just make a new RgbChromosome and set it’s R, G and B values to the same value as the parent chromosome, added a random value between -5 and 5. The Math.Max and Math.Min juggling is to avoid negative and 255+ values.

protected override IEnumerable<IChromosome<Rgb>> Mutate(IChromosome<Rgb> chromosome)
{
	RgbChromosome mutation = new RgbChromosome(chromosome.ChromosomeValue.R, chromosome.ChromosomeValue.G, chromosome.ChromosomeValue.B);
	mutation.ChromosomeValue.R = Math.Min(255, Math.Max(0, mutation.ChromosomeValue.R + random.Next(-5, 6)));
	mutation.ChromosomeValue.G = Math.Min(255, Math.Max(0, mutation.ChromosomeValue.G + random.Next(-5, 6)));
	mutation.ChromosomeValue.B = Math.Min(255, Math.Max(0, mutation.ChromosomeValue.B + random.Next(-5, 6)));

	yield return mutation;
}

The RgbChromosome

The final class is the one implementing the IChromosome interface.

class RgbChromosome : IChromosome<Rgb>

In this case I’ve hardcoded a target RGB value that we wish to guess. Note that this is only for demonstrations sake - usually in genetic algorithms we don’t know the “answer” and will therefor have to base the fitness function on a set of rules that evaluate the fitness of the candidate.

private Rgb targetRgb = new Rgb { R = 127, G = 240, B = 50 };

The fitness function calculates the total difference in RGB values and subtracts that from the maximum difference. As a result, we get a fitness value with lower values indicating a worse solution.

public double Fitness
{
	get
	{
		int maxDiff = 255 * 3;

		int rDiff = Math.Abs(chromosome.R - targetRgb.R);
		int gDiff = Math.Abs(chromosome.G - targetRgb.G);
		int bDiff = Math.Abs(chromosome.B - targetRgb.B);
		int totalDiff = rDiff + gDiff + bDiff;

		return maxDiff - totalDiff;
	}
}

Here is the full IChromosome implementation:

class RgbChromosome : IChromosome<Rgb>
{
	private Rgb targetRgb = new Rgb { R = 127, G = 240, B = 50 };
	private Rgb chromosome;

	public RgbChromosome(int r, int g, int b)
	{
		this.chromosome = new Rgb { R = r, G = g, B = b };
	}

	public double Fitness
	{
		get
		{
			int maxDiff = 255 * 3;

			int rDiff = Math.Abs(chromosome.R - targetRgb.R);
			int gDiff = Math.Abs(chromosome.G - targetRgb.G);
			int bDiff = Math.Abs(chromosome.B - targetRgb.B);
			int totalDiff = rDiff + gDiff + bDiff;

			return maxDiff - totalDiff;
		}
	}

	public Rgb ChromosomeValue
	{
		get { return chromosome; }
	}
}

Running the algorithm

Running the algorithm is as simple as instantiating a new RgbGuesser and then calling PerformEvolution on it repeatedly. Note that there’s no built in stop criteria in the algorithm, so it’ll continue to evolve the candidates even though a perfect candidate may already have been evolved. This I’ve introduced a simple check to see whether a perfect candidate exists:

if (topChromosomes.Where(c => c.Fitness == 255 * 3).Count() > 0)

The full code can be seen below:

// Setup RgbGuesser
RgbGuesser rgbGuesser = new RgbGuesser();

// For each generation, write the generation number + top 5 chromosomes + fitness
for (int i = 1; i < 100000; i++)
{
	Console.WriteLine("Generation: " + rgbGuesser.CurrentGenerationNumber);
	Console.WriteLine("-----");

	// Get top 5 chromosomes
	var topChromosomes = rgbGuesser.CurrentGenerationPopulation
		.OrderByDescending(c => c.Fitness)
		.Take(5);

	// Get bottom 5 chromosomes
	var bottomChromosomes = rgbGuesser.CurrentGenerationPopulation
		.OrderBy(c => c.Fitness)
		.Take(5);

	if (topChromosomes.Where(c => c.Fitness == 255 * 3).Count() > 0)
	{
		Console.WriteLine();
		Console.WriteLine();
		Console.WriteLine();
		Console.WriteLine("### Perfect match found at generation " + rgbGuesser.CurrentGenerationNumber + "!");
		Console.Read();
		return;
	}

	// Print out top 5 and bottom 5 chromosomes
	foreach (var chromosome in topChromosomes)
		Console.WriteLine(Convert.ToInt32(chromosome.Fitness).ToString().PadLeft(3) + ": " + chromosome.ChromosomeValue);
	Console.WriteLine("-----");
	foreach (var chromosome in bottomChromosomes.OrderByDescending(c => c.Fitness))
		Console.WriteLine(Convert.ToInt32(chromosome.Fitness).ToString().PadLeft(3) + ": " + chromosome.ChromosomeValue);

	Console.WriteLine();
	Console.WriteLine();

	// Homage to Charles Darwin
	rgbGuesser.PerformEvolution();
}

Console.WriteLine("Done");
Console.ReadLine();

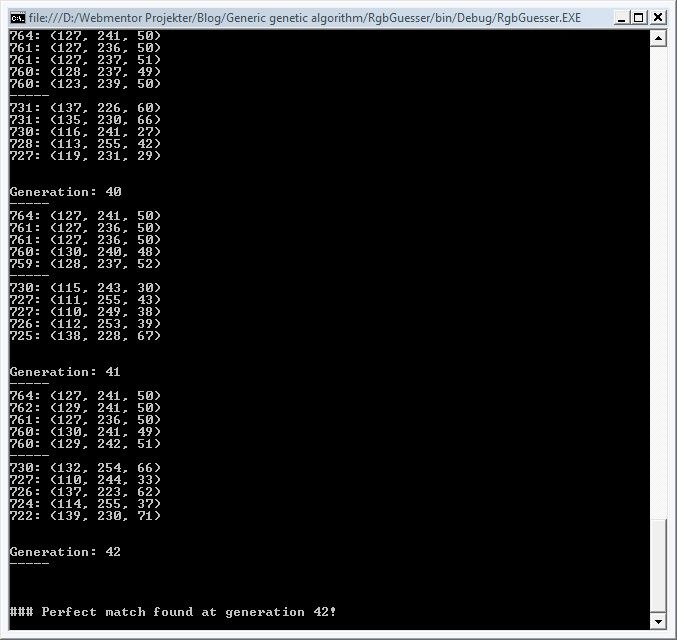
Running the application should eventually result in a perfect candidate being found. If you’re lucky, you’ll find it at generation 42 :)

Doing the numbers

There are different ways of guessing an RGB value. We could just randomly guess until we hit the correct one - with a probability of 1/(255^3).

We could also iterate over all 255^3 solutions, eventually hitting one. Provided the target is completely random, we should hit it after 50% of the solutions have been tested - that is, after just about 8 million tests.

Another more clever approach, given the fitness function would be to just increment each RGB value once and fine the point at which an increment results in a lower score - then we’ve solved one of the RGB values. Using this approach, we can solve the problem in just 255*3 number of tries at most. But really, that’s no fun!

Based on a quick series of tests, 50 seems to be the average max generation we’ll have to hit before we’ve guess the correct RGB value. That’s 50 generations of 100 candidates, for a total candidate count of 5000 - somewhat less than the random guessing and iterative solutions. To conclude - in this case, a genetic algorithm is far from the optimal solution, but it’s an interesting way of approaching hard-to-define problems that may not have a single optimal solution that can be calculated within a certain time restraint. In those cases genetic algorithms can be a great way of approximating a close-to-perfect solution.

Update

Based on some of the comments I’ve received, I’ve posted an update to the genetic algorithm to make it more “genetic”.

Downloads

Sample solution code:
GeneticTesting.zip